Board Cycles, the Dreamboard and Shifts
Board Cycles
Damien Moore (Canada) scored 18 seconds on Intermediate, 22 Mar 2000.
Gernot Stania (Germany) set a world record of 15 seconds on Intermediate, 20 May 2000.
A week later, Lasse Nyholm (Denmark) noticed that we had played our games on the same board!
A search revealed that others had also made records on this board, leading to the discovery of the Dreamboard. It was suggested that Minesweeper generated random boards but started from the same game when installed. Everyone would get the same boards in the same order and would have one chance at each board.
However, Gernot broke the record again in November, with 12 on the Dreamboard again!
New theories were developed. Perhaps board generation was based on the time you opened Minesweeper, such as the fraction of a second you start the game. If someone opened the game on the same hundredth of a second, they would get the same series of random boards. The Dreamboard would be near the beginning of that series. Another theory was that board generation is not infinite nor random, but is a finite cycle.
David Barry (Australia) proved the second theory to be true in December of 2002. He wrote a small program that repetitively started games and looked for board matches. His first discovery was that more than one cycle existed! His second discovery was that the Dreamboard cycle seemed to only have 12096 boards. Unfortunately there was a problem with his program that prevented a complete investigation.
This has led to many theories on the algorithm used to generate boards. This article explores a lesser known fact about the Dreamboard and Board Cyles: Shifts.
Shifts
After the Dreamboard was discovered people noticed that some games overlapped it. Two similar games were discovered, easily recognised by the distinctive red 333 pattern. This led to a new theory suggesting that each cycle shifted a set amount from the previous cycle. In effect, cycles were a massive recycling program.
I found a third Dreamboard shift 10 Oct 2004 that seemed to include only part of the bottom two rows. This was exciting, because it seemed to match a theory I had kept secret: What if there was an finite Minesweeper grid from which all intermediate games are just 16x16 sections?
I spent a day in Paint pasting together matching sections of these shifts, and discovered something completely different!
| This is the new shift. | This is another. |
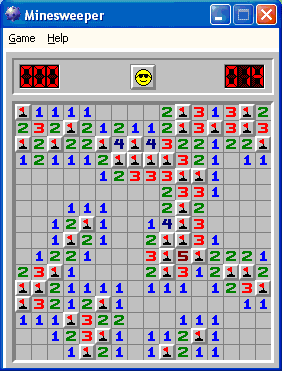 |
 |
| And another. | This is the Dreamboard. |
 |
 |
These are not four different boards...they are all the Dreamboard! I thought that pasting the boards would start a map, eventually revealing a grid from which all games are cut.
The Dreamboard comes from an infinite grid...but there are only 256 unique squares! This 16x16 tile infinitely repeats. You can choose any square in the tile, count 16 squares in any direction, and find that exact square again.
Here is the tiled picture:

| This is the Dreamboard. | This is the tile, the real Dreamboard. |
 |
 |
The Dreamboard and its shifts are a single tile! Notice how every number on an edge counts mines on the opposite edge. Each time you shift a row, the last row falls off and becomes the new first row. Shifting makes 256 boards possible from the same tile, and all infinitely repeat.
However, there are not 256 shifts: there are 4.
What is the evidence?
First, there are only 4 known shifts after four years. Secondly, pasting these 4 shifts into the grid reveals something very interesting:

The Dreamboard is the blue tile. You can match the others. I have highlighted the most important square: everything literally hinges on this.
If the yellow tile is a graph, the bottom left corner is (0,0), and the important square is (7,5). Shift the yellow square 2 up, rotate 90 degrees on this dot, and you get the blue square. Shift the blue tile 2 left, rotate 90 degrees again, and you get the green square. Shift green 2 down, rotate 90 degrees, you get the red square. Shift red 2 right, rotate 90 degrees, and you are back to yellow. (This is the same as shifting 4 up 4 down, 2 down 6 left, 4 up 6 left, 2 down 4 right).
If you view the situation from the center dot, you shift out 2, in 2, out 2, in 2 while rotating 90 degrees around (7,5). The grid does not rotate, only the 16x16 box. Whatever part of the grid lies beneath becomes the new board.
Thirdly, if you have doubts look at this other example:
| Sebastian Schmidt | Elmar Zimmermann |
 |
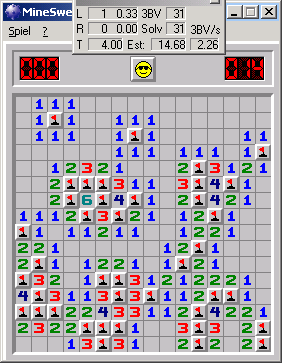 |
| George Strain | Damien Moore |
 |
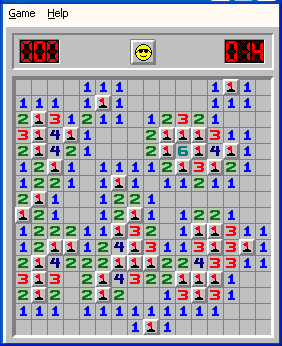 |
Here is the tiled grid with their locations marked:

It is the same pattern.
Considering that David Barry proved finite cycles exist, I suggest that there are only 4 cycles.
I know nothing about programming, but it makes sense. Food for thought. Luck!